我们先考虑二维的向量,向量的表示和坐标很像,(10,20)对坐标而言,就是一个固定的点,然而在向量中,它意味着x方向行进10,y方向行进20,所以坐标(0,0)加上向量(10,20)后,就到达了点(10,20)。
向量可以通过两个点来计算出来,如下图,A经过向量AB到达了B,则向量AB就是(30, 35) – (10, 20) = (20, 15)。我们也能猜到向量BA会是(-20, -15),注意向量AB和向量BA,虽然长度一样,但是方向不同。

向量运算
我们观察下图,点A出发,通过向量AB到达B点,B通过BC到达C;由A出发的话,经向量AC就直接到达C。
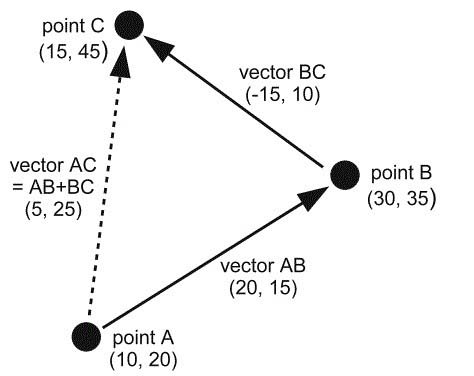
由此我们得到一个显而易见的结论向量AC = 向量AB + 向量BC。向量的加法计算方法呼之欲出:
(20, 15) + (-15, 10) = (20-15, 15+10) = (5, 25)
把各个方向分别相加,我们就得到了向量的加法运算法则。很类似的,减法也是同样,把各个方向分别想减。
有加减法,那乘除法呢?
用一个向量来乘(除)一个数,其实际意义就是,向量的方向不变,而大小放大(缩小)多少倍。
向量的运算被广泛的用来计算到达某个位置时的中间状态,比如我们知道一个角色从A到B,中间有10帧,那么很显然的,把向量通过(B-A)/10计算出来,每次将角色移动到当前位置就可以了,很简单吧?
本站内容未经许可,禁止任何网站及个人进行转载。










