杨辉三角相信很多人都不陌生,它是一个无限对称的数字金字塔,在中国南宋数学家杨辉1261年所著的《详解九章算法》一书中出现。在欧洲,帕斯卡(1623—-1662)在1654年发现这一规律,所以这个表又叫做帕斯卡三角形。帕斯卡的发现比杨辉要迟393年,比贾宪迟600年。

在初中,我们就知道,杨辉三角的两个腰边的数都是 1,其它位置的数都是它顶上两个数之和。这就是我们编程实现杨辉三角的关键之一。
使用scratch编写这个程序相对于别的语言来说要更复杂一点,复杂的不是算法,而是如何展示出来,下面我们先来分析一下这个程序有哪些难点,面对这些困难我们如何克服。这就是我们所强调的,少儿编程应该重点学习如何解决问题,如何利用有限的资源去做更多的事。
问题1:找规律,将现象转为数据
杨辉三角的两个腰边的数都是 1,其它位置的数都是它顶上两个数之和。
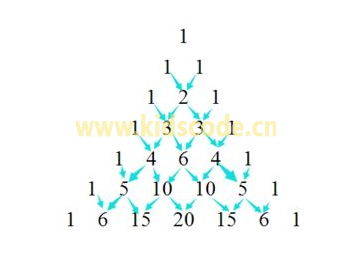
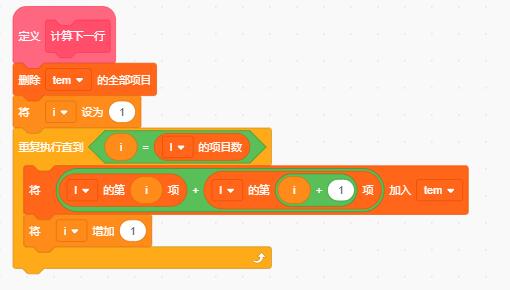
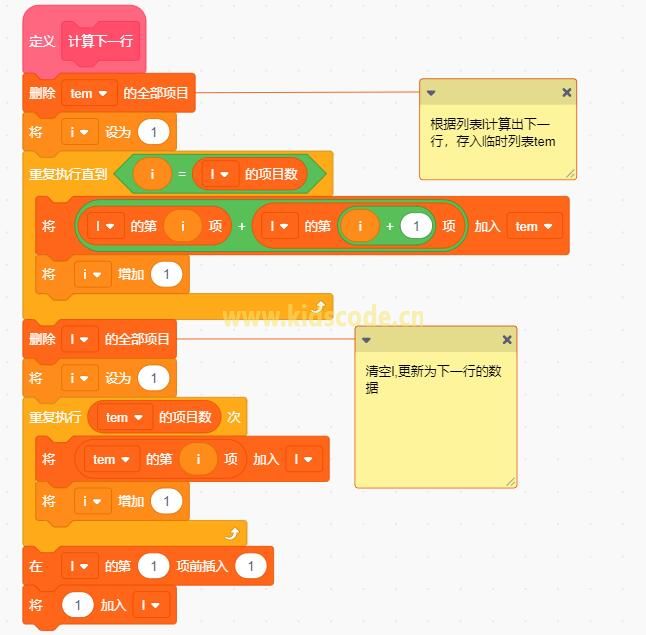
如图所示,我们可以利用上一行的结果,计算出下一行的数据。因此定义两个列表(l:上一行数据;tem:下一行数据),每个列表用来存储一行数据:

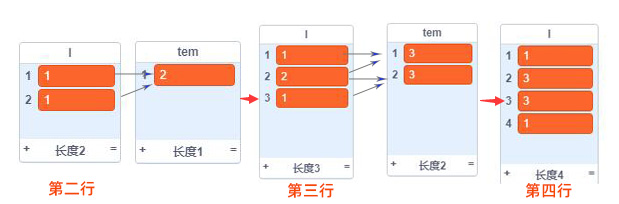
如图,给tem首位加上1,就是1,2,1那就是第三行的数据,接下来再把l的数据清空,将tem的数据存储到l里,并在首位添加1,如此循环就可以一层一层的输出了。

问题二:如何将数字打印显示到舞台?
上面解决了数据问题,下面就要把列表l里的数据一个个显示到舞台上,这就是scratch的麻烦所在,无法直接打印字符。于是想办法,用数字角色,添加造型,将0-9都包括进去,根据不同的数字切换不同的造型,利用画笔里的图章或者克隆将这个数留在舞台上,为了简单,就用图章吧。
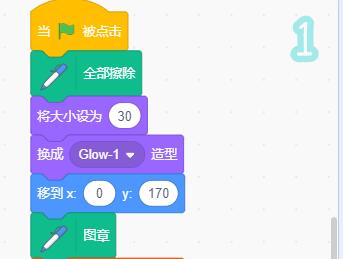
问题三:换行后位置如何确定?
第一行很好确定,就在舞台中央的正上方,那换到下一行从哪里开始呢?这需要我们根据实际情况去测试一下,如下图所示,找到这个合适的间距。
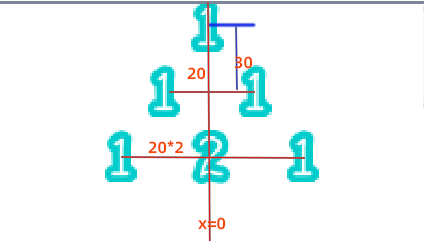

上下间距设置为30,即y坐标-30,x坐标向左移动,第二次左移20,第三层左移40,第四层就是60,总结规律就是0-(层数-1)*20,数字与数字之间的距离设置为30。
问题四:如果数字大于9怎么办?
比如要打印出10,这怎么办?我们的角色造型里没有这么多,我们只有0-9。这时就想到了拆分,将多位数一位一位的拆出来(将0造型放在最后,即:换成0造型,默认就是最后一个造型)。
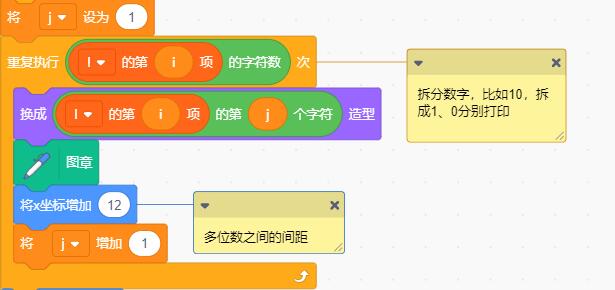
目前所有遇到的问题基本都有了解决办法,我们就可以开始动手构建整个程序了。,第一行是1,这个是固定的,我们直接在开始用图章印上去,从第二行开始,重复执行打印,计算下一行,流程如下。
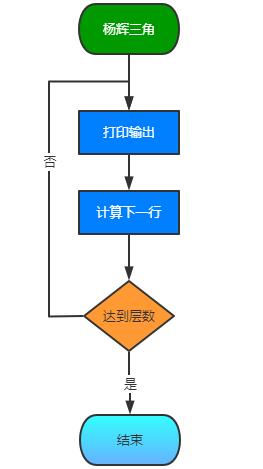
完整的程序如图
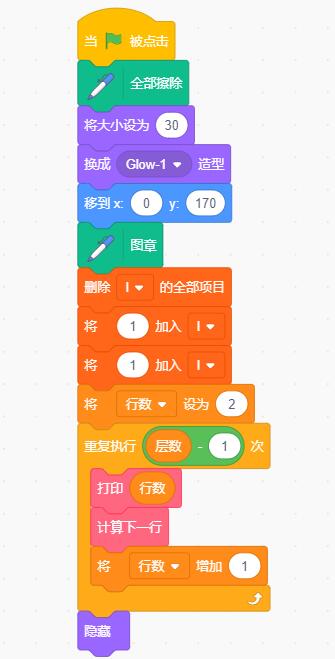
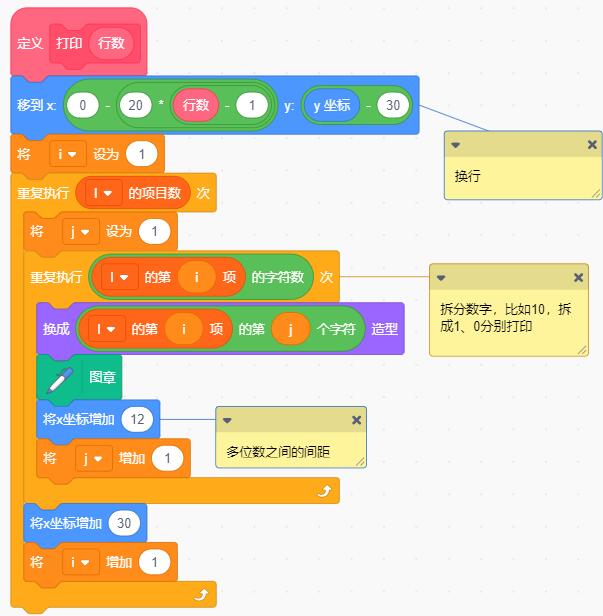
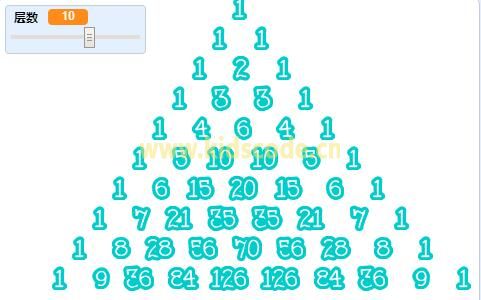
运行结果:
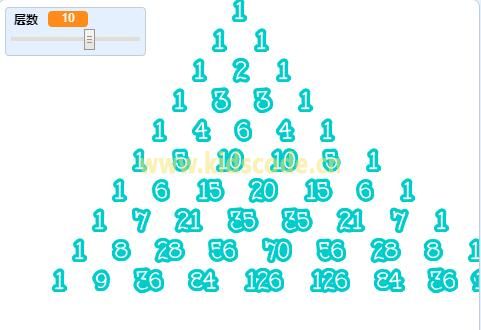
效果优化:
从图中看到结果并不是我们想要的等腰三角形效果,因为后面数字变大,占据的宽度增加,所以整体向右偏移,因此就要对这些多位数进行处理,让他们起始位置向左移动一点,这样就可以了。
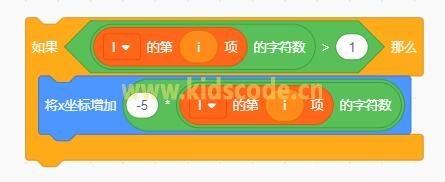
优化后的积木:
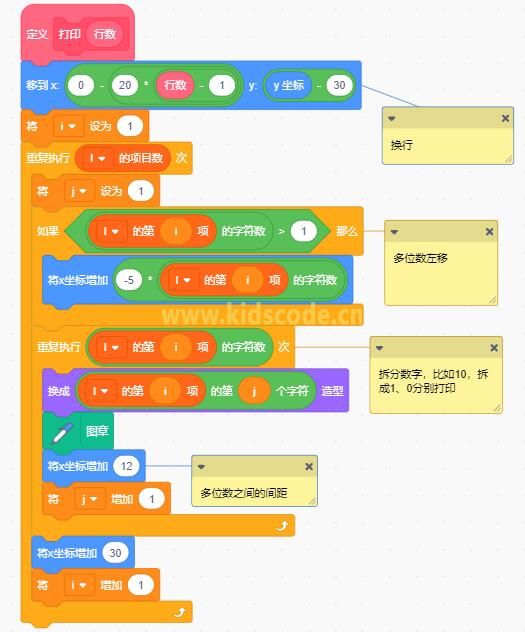
在高中我们会学到,杨辉三角中的任何一个数都等于一个组合数,如果有兴趣可以利用这一公式来做。
本站内容未经许可,禁止任何网站及个人进行转载。











