少儿编程网

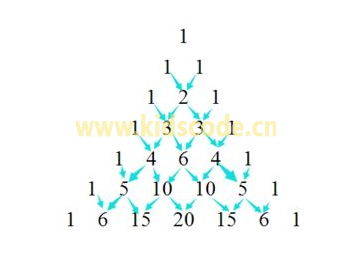
杨辉三角（也称帕斯卡三角），它是一个无限对称的数字金字塔，从顶部的单个1开始，下面一行中的每个数字都是上面两个数字的和。

题目：打印出杨辉三角形（要求打印出10行如下图）。　

分析：

把每一行看作一个列表,不断输出下一行的列表。

对于每一行，列表的第一个元素和最后一个元素是不变的。如果用空列表L = [] 表示的话，第n行 L[0], L[n],是 不变的，

第一步：先找规律，抽象化问题：

首先可以观察到，第一行为[1]，我们直接赋给一个变量：初始化数列 p = [1]

其次我们观察到，下面的每一行的开头结尾都是[1],那么我们可以推导出每一行的规律为：[1]+.........+[1]

那么我们发现，从第三行开始中间的 [2]，第四行中间的 [3，3]，第五行中间的 [4,6,4] 等等以此类推才是我们需要推导的部分

第一行：[1] 设 p = [1]

第二行：[1] [1] 设 p = [1,1]

第三行：[1] [2] [1] 设 p = [1,2,1]

第四行：[1] [3] [3] [1]设 p = [1,3,3,1]

经过找规律，可以发现，每一个新的列表中间的部分，都等于上一行列表的：第0个元素+第1个元素，第1个元素+第2个元素，第2个元素+第3个元素,.......

加上头尾也就是[1] [p[0]+p[1]] [p[1]+p[2]]..... [1]

比如上面第三行：p[0] = 1, p[1] = 2, p[3] = [1]

后面以此类推

既然核心点是这个除去首位两个 [1] 的中间部分：[p[0] + p[1]] [p[1] + p[2]] [p[2] + p[3]]........

我们很容易得到规律：[p[i] + p[i+1]]# for i in range(x)

程序代码：

def yanghuisanjiao(n):

   print([1])

   line = [1,1]

   print(line)

   for i in range(2,n):

       l=[]

       for j in range(0,len(line)-1):

           l.append(line[j]+line[j+1]) #除去首尾中间的数字

       line = [1]+l+[1] #加上首尾完整的一行

       print(line)

yanghuisanjiao(10)

本站内容未经许可，禁止任何网站及个人进行转载。