对于本题目我们将会通过scratch使用不同的方法来求解,通过分析来不断优化(简单的说就是让计算机使用更短的时间与最小的计算量来完成),最终简单的得出结果。这个题目有一定难度建议12岁以上的孩子学习,如果条件允许的话,希望家长能够先理解然后给予孩子以指导和帮助。
题目:
有一座高度是10级台阶的楼梯,从下往上走,每跨一步只能向上1级或者2级台阶。要求用程序来求出一共有多少种走法。
比如,每次走1级台阶,一共走10步,这是其中一种走法。我们可以简写成 1,1,1,1,1,1,1,1,1,1。
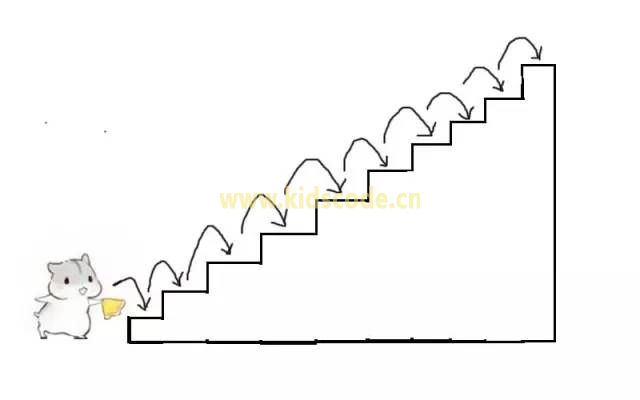
再比如,每次走2级台阶,一共走5步,这是另一种走法。我们可以简写成 2,2,2,2,2。
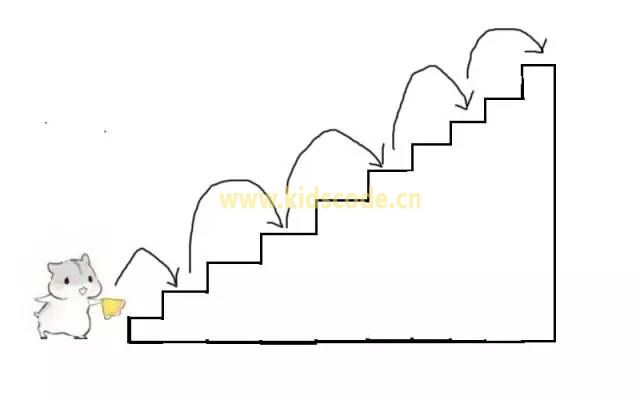
当然,除此之外,还有很多很多种走法。






第一种情况:

第二种情况:










F(1) = 1;
F(2) = 2;
F(n) = F(n-1)+F(n-2)(n>=3)



什么是递归?>>>画雪花曲线-scratch中的递归
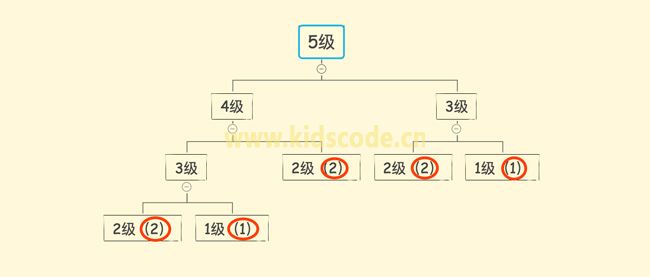
按照递归的思路,可以把这个题目的求解过程归纳为下图:

比如有5级台阶:最终的方法就是2+1+2+2+1=8
scratch程序实现:
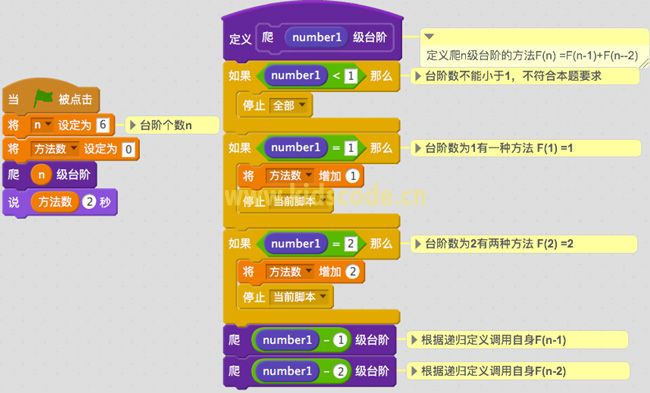
源码下载请用电脑打开:scratch爬台阶问题求解(递归求解)
动漫:伯乐专栏作者/玻璃猫
本站内容未经许可,禁止任何网站及个人进行转载。











