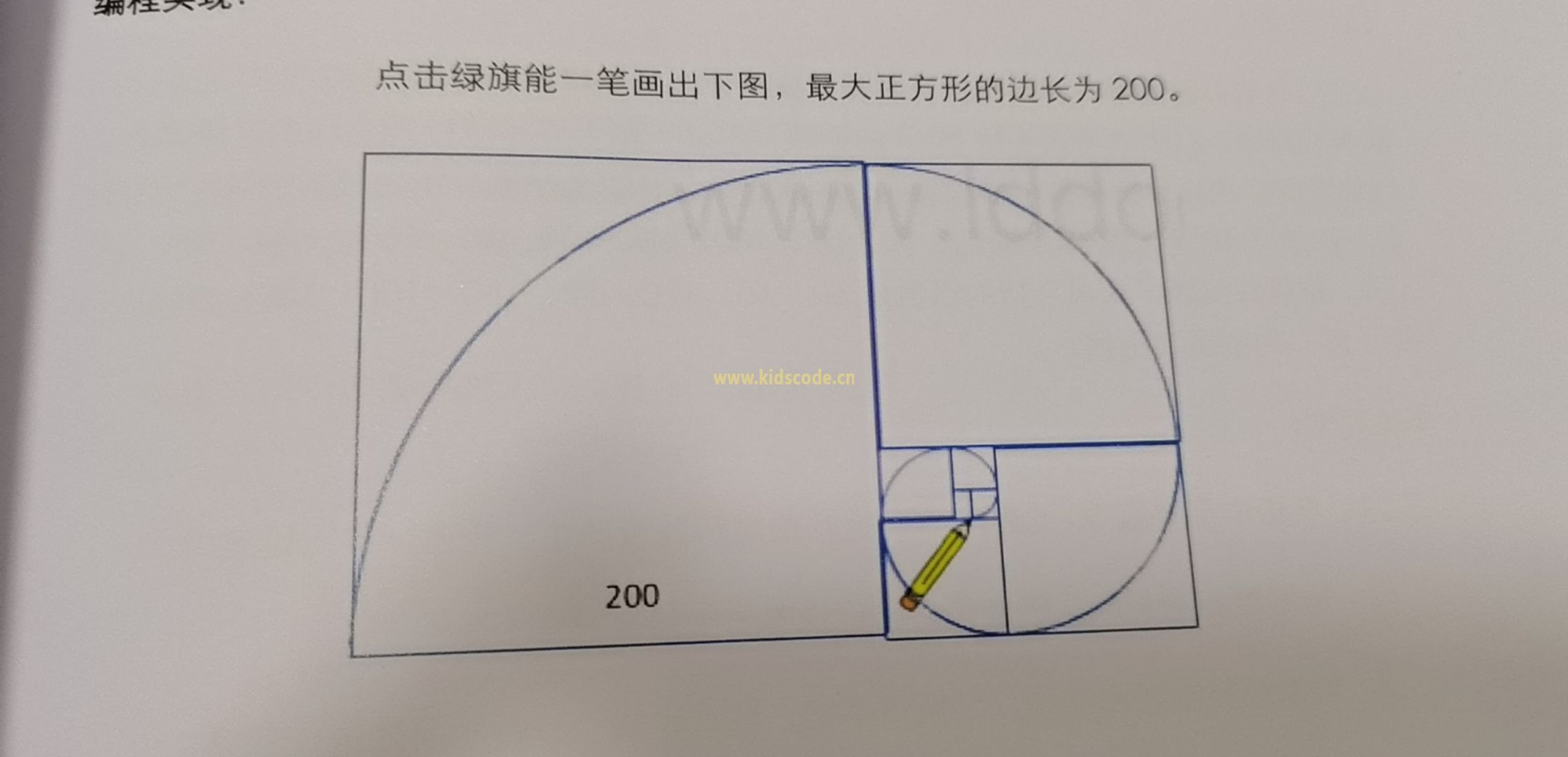
方法一:简单模拟
思路:每画一个四分之一圆弧,可以将让其移动n步,旋转1°,重复执行90次; 通过改变移动步数变量(n)来实现圆大小的变化,移动步数变量(n)根据斐波那契数列生成即可。
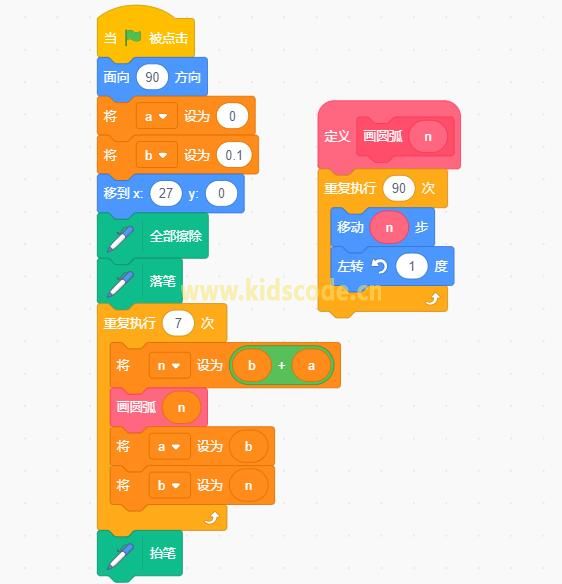
这种方法比较简单,能够模拟出这种曲线,但是数据并不准确,因为通过改变移动步数旋转画出的圆弧,虽然大小发生了变化,但是这并不是准确改变半径的方法。

该方法适简单易懂,适合初学者,可以达到练习的目的。
方法二:圆的标准方程
这个方法是根据数学公式来严格画圆弧的,相对来说会复杂一点,大体思路与代码如下:
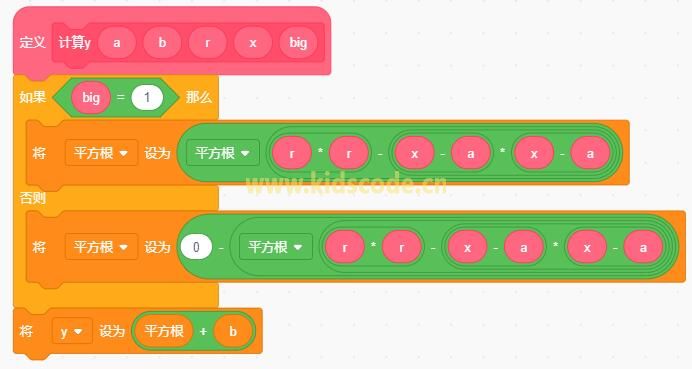
1、根据圆的标准方程:(x-a)2+(y-b)2=r2,来画圆弧。方程有三个参数a、b、r,即圆心坐标为(a,b),r是圆的半径。根据方程推导出x,y的关系:
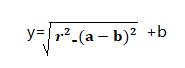
这个公式中有平方根,那这个y的取值到底是哪个?如何确认?
观察下图(画笔从内往外画)
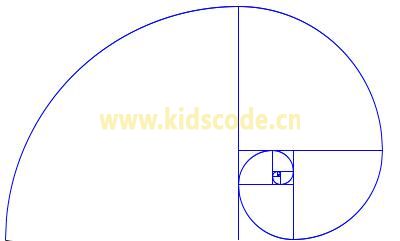
会发现,如果x的值增大,圆弧在下侧,y的值取小(及平方根取负值),x值减小圆弧会在上侧,及y的值取大
通过循环不断改变x的值,得到一系列点(x,y)把他们连接起来就画出了圆弧。
2、半径我们已经知道遵循斐波那契数列的规律,那下一个圆弧的半径就可以确定了,就让圆上的点向圆心的方向移动半径距离,就可以获得当前圆心的坐标了。
具体怎么确定圆心在哪个方向,我们可以画图看一下,
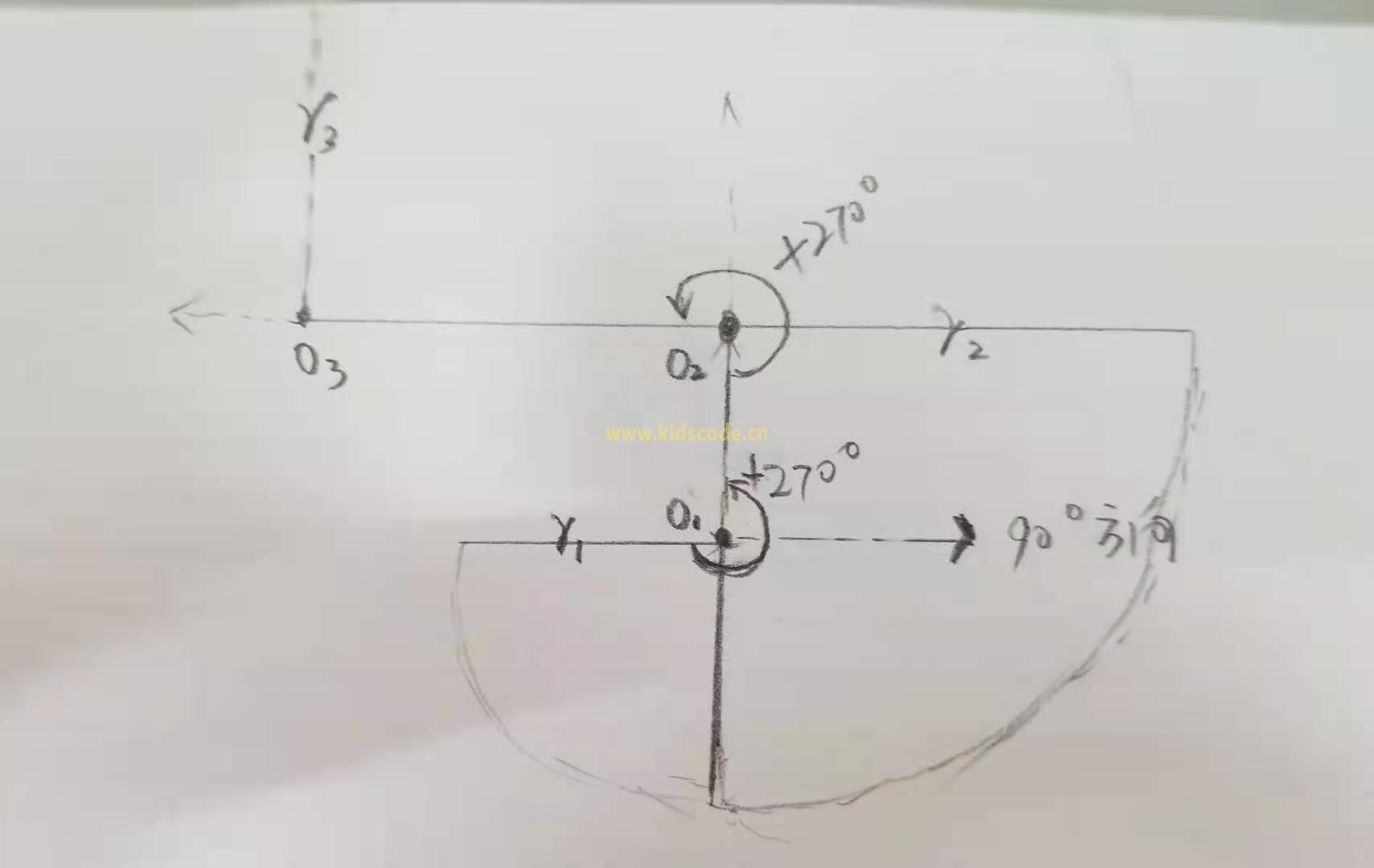
从草图中有三个圆心分别是O1、O2、O3,画笔每画四分之一圆弧后,它的方向就要增加270°,那才是圆心的方向。
下面是程序的截图:
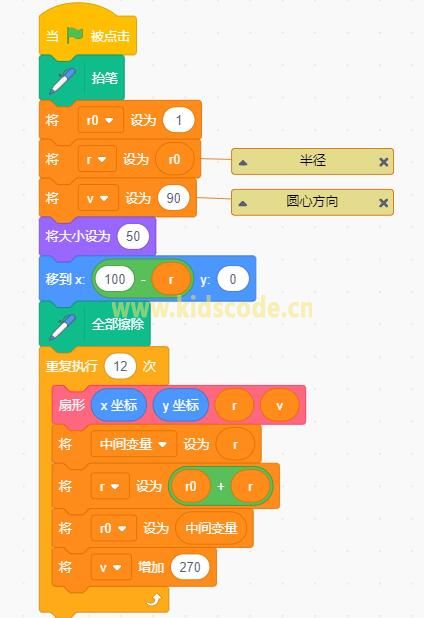
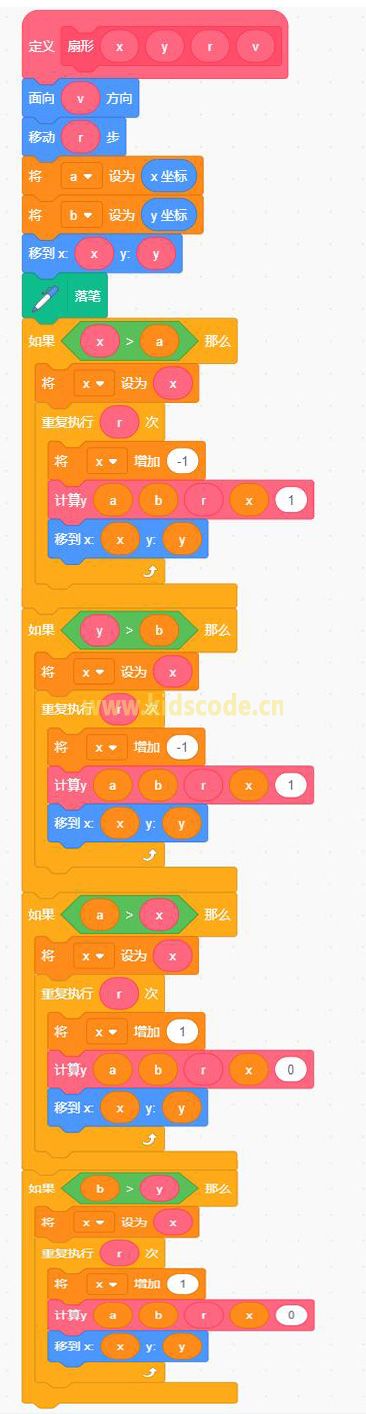
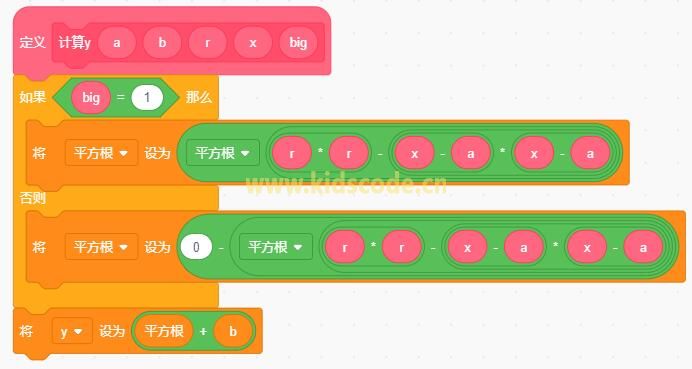
程序源码及下载:
本站内容未经许可,禁止任何网站及个人进行转载。











