上一节动脑:NOIP爬台阶问题求解【上】我们学会了如何使用递归来解决这个问题,现在我们来进一步优化(简单的说就是让计算机使用更短的时间与最小的计算量来完成),如果上一节的递归程序实现部分你没理解,没关系,并不影响本节的学习。这个题目有一定难度建议12岁以上的孩子学习,如果条件允许的话,希望家长能够先理解然后给予孩子以指导和帮助。
题目:有一座高度是10级台阶的楼梯,从下往上走,每跨一步只能向上1级或者2级台阶。要求用程序来求出一共有多少种走法。

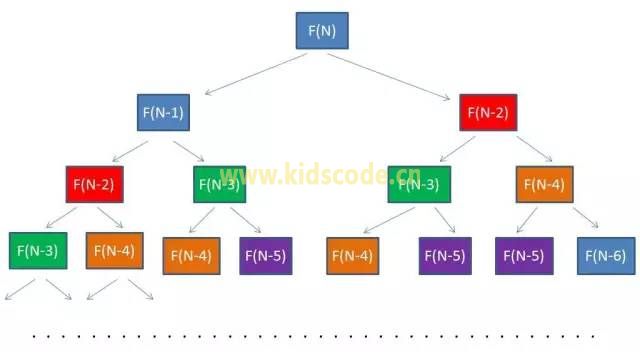
观察上图,颜色相同的都是被重复计算的。


















分两种情况,台阶数小于3,如果是1级,那么只有一种走法,如果是2级那么有2种走法,当大于2级,就用到我们上面总结的规律重复的往后推算。第n级F(n)=F(n-1)+F(n-2)

这个代码看起来是不是比递归容易理解多了,而且还提高了效率呢。

如果你坚持看到这里,并且理解了这个解题的思路(对scratch程序没理解,没关系,这不是重点),那么恭喜你,你在不知不觉中学到了一个高大上的新技能——动态规划。




怎么样?看完有没有收获呢?
本站内容未经许可,禁止任何网站及个人进行转载。