蒙特卡洛算法是以概率和统计的理论、方法为基础的一种计算方法,将所求解的问题同一定的概率模型相联系;用电子计算机实现统计模拟和抽样,以获得问题的近似解,故又称统计模拟法或统计实验法。
蒙特卡洛算法:蒙特卡洛是美国摩纳哥的一个城市,以赌博闻名于世。蒙特卡洛算法借用这一城市的名称是为了象征性的表明该方法的概率统计特点。蒙特卡洛算法作为一种计算方法,是由S.M.乌拉姆和J.冯诺依曼在20世纪40年代中叶为研制核武器的需要而提出的。
蒙特卡洛方法的基本思想虽然早已被人提出,例如在古典概率中的著名法国数学家布丰利用投针求圆周率Pi值,却很少被使用。直到电子计算机出现后,使得人们可以通过电子计算机来模拟巨大数目的随机试验过程,使得蒙特卡洛方法得到广泛地应用。
用蒙特卡洛投点法计算π的值
在一个边长为a的正方形内一均匀概率随机投点,该点落在此正方形的内切圆中的概率即为内切圆与正方形的面积比值,π/4
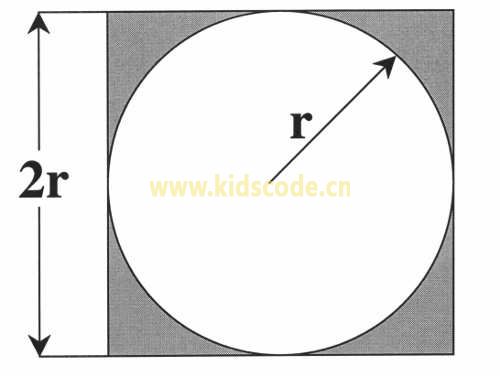
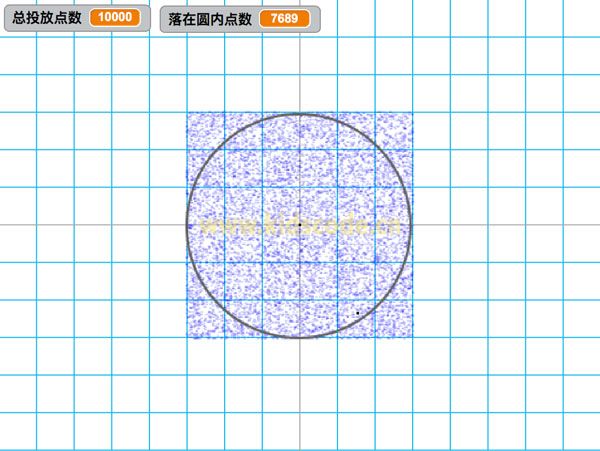
现在,在这个正方形内部,随机产生10000个点,计算它们与中心点的距离,从而判断是否落在圆的内部。如果这些点均匀分布,那么圆内的点应该占到所有点的 π/4,因此将这个比值乘以4,就是π的值。
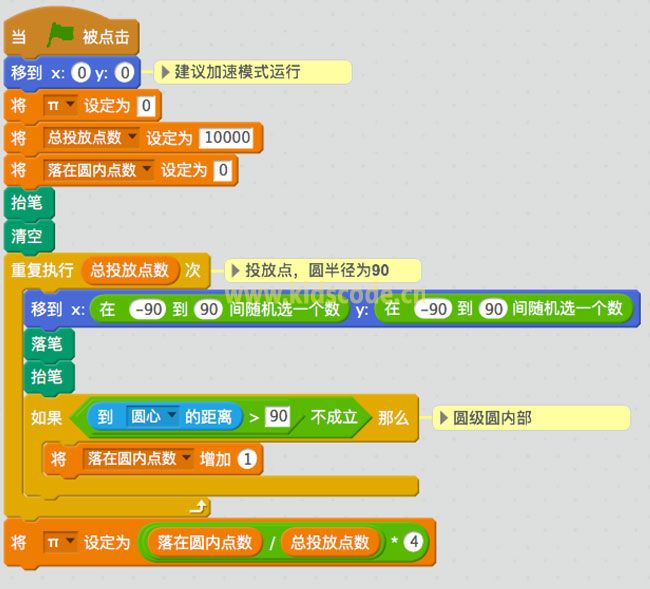
源程序下载:scratch利用蒙特卡罗方法计算圆周率
从实验结果可以分析得出:
1.随着投点的次数增加,圆周率π计算的准确率在增加;
2.但当次数达到一定规模时,准确率精度增加在减缓,其原因是生成的随机数是伪随机的,这也是蒙特卡洛算法达不到祖冲之求圆周率精度的内在原因;
3.同时在进行100000次投点中也可以发现,对于相同的投点数由于实验本身的随机性每次的实验结果是不同的。
本题目由会员:赣州-rax 分享而来,表示感谢。
本站内容未经许可,禁止任何网站及个人进行转载。











