在开始介绍雪花曲线的画法之前我们先来认识一个术语“递归”(递归概念比较简单,但是实际运用中理解起来还是有难度的)
什么是递归?
一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法被称为递归,递归做为一种算法在程序设计语言中广泛应用。 那么这句话怎么理解呢?我们来scratch来做一个例子看一下。
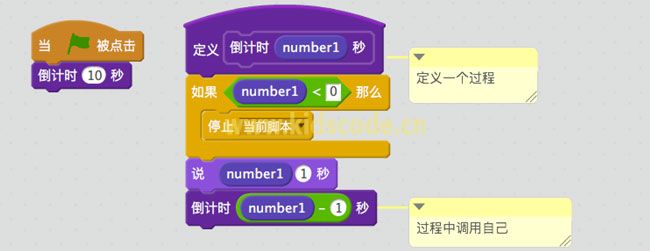
图中我们自定义了一个模块(过程)倒计时,在定义这个过程中直接调用了自身倒计时,直到数字小于0.
我们再来看看其他人怎么理解这个递归的吧。
递归就是包子馅的包子。它的极限是馒头。
山上有座庙:
从前有座山,山上有个庙,庙里有个老和尚,有一天,老和尚给小和尚讲故事。讲的故事是:山上有座庙
再看两张图:


当两面镜子相互之间近似平行时,镜中嵌套的图像是以无限递归的形式出现的。也可以理解为自我复制的过程。
好了,下面开始我们的正式内容,画雪花曲线。
请提前了解什么是雪花曲线?http://www.kidscode.cn/archives/5300
由于雪花曲线是从三角行不断变换得到,因此我们绘制雪花曲线之需要关注一条边的变化规律即可,想办法画出来,另外两条边都是完全一样的。下面我们从0级开始,看看这个三角形底边是如何一级一级发生变化的。

0级(三角形):画直线

1级:0级(1/3长度)右转60度 0级(1/3长度)左转120度 0级(1/3长度)右转60度 0级(1/3长度)

2级:1级(1/3长度)右转60度 1级(1/3长度) 左转120度 1级(1/3长度) 右转60度 1级(1/3长度)

3级:2级(1/3长度)右转60度 2级(1/3长度) 左转120度 2级(1/3长度) 右转60度 2级(1/3长度)
依次类推:
4级:3级(1/3长度)右转60度 3级(1/3长度) 左转120度 3级(1/3长度) 右转60度 3级(1/3长度)
...
n级:n-1级(1/3长度)右转60度 n-1级(1/3长度) 左转120度 n-1级(1/3长度) 右转60度 n-1级(1/3长度)
我们发现了这样的规律那么在程序中该怎么写呢?这里就用到了我们开始所讲到的递归。
打开scratch->更多积木->添加新的积木块:我们自定义一个模块“绘制边”这里需要两个参数,一个是变化的级数,另一个是长度,如果是0级就直接绘制一个线段停止,否则就按照上面的规律:级数-1级(1/3长度)右转60度 级数-1级(1/3长度)左转120度 级数-1级(1/3长度)右转60度 级数-1级(1/3长度)
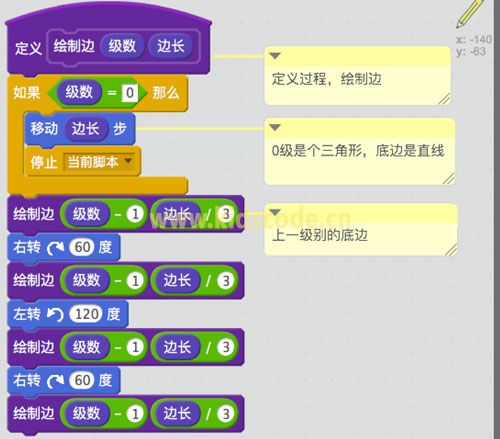
这样这个程序的核心部分就完成了,代码很简洁,不过理解起来有点难,需要多去想想理解。
画边的程序做好了,我们只需要像画三角形一样,拼接起来即可。接下来我们来完成这个程序,画出这个曲线吧。
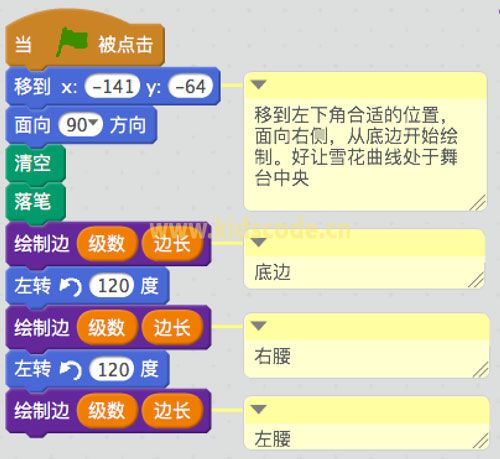
程序源码下载(用pc端打开):http://www.kidscode.cn/product/5374
本站内容未经许可,禁止任何网站及个人进行转载。











