编程实现: 现将某区域的地图变成一个平面的方格图,平面上有n处居⺠住宅,已知n处居⺠住宅,每处居 ⺠住宅位置所处的行数和列数,现计划设置一处便⺠办事处,使办事处去到各个住宅位置的距离 之和最短(只能上下左右走,且办事处可以和住宅处在同一个方格),请问最短距离之和是多少?
例如:共有两处居⺠住宅,位置如下图:
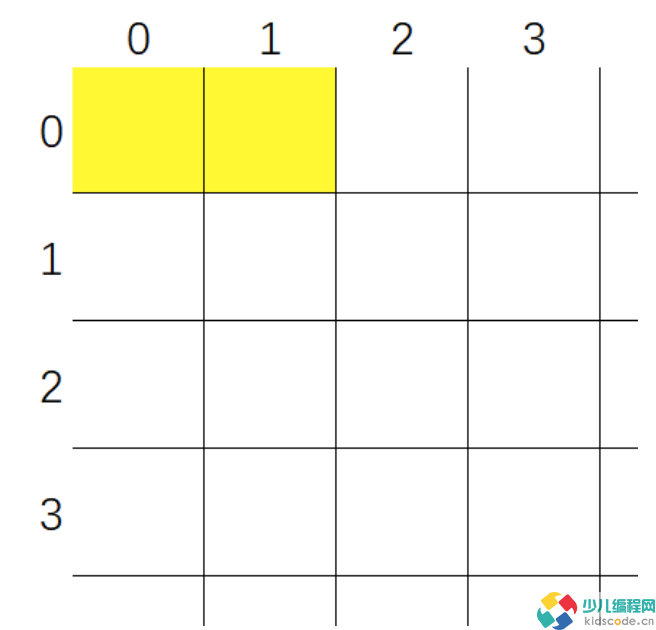
第一处居⺠住宅在0行0列,第二处居⺠住宅在0行1列,那么办事处可设置在0行0列 处,到第一处居⺠住宅的距离为0,到第二处居⺠住宅的距离为1,最短距离之和为1。
输入描述
第一行输入一个正整数n,表示有n处居⺠住宅(1≤n≤10000)。 第二行往后n行,每一行输入一对数字,表示每处居⺠住宅的行数和列数(0≤行数<100,0≤列 数<100),中间用空格隔开。
输出描述
输出最短距离之和。
输入样例
2
00
01
输出样例
1
思路:
通过遍历平面方格图的每一个位置,计算在该位置设置便民办事处时到所有居民住宅的距离(曼哈顿距离)之和,然后找出距离之和最短的那个值。
实现步骤:
1. 输入
首先,通过input()函数获取居民住宅的数量n,它决定了后续要输入多少组居民住宅的坐标信息。
接着,使用一个循环让用户依次输入每处居民住宅所处的行数x和列数y,并将这些坐标以元组的形式添加到houses列表中,这个列表就存储了所有居民住宅的位置信息。
2. 计算距离总和并寻找最小值部分
初始化一个变量min_distance_sum为正无穷大(float('inf')),用于后续比较并记录最短的距离之和。
然后通过两层嵌套的循环来遍历整个方格图的每一个可能位置。对于每一个位置(用(row, col)表示):
初始化一个变量distance_sum为 0,用于记录当前位置到所有居民住宅的距离之和。
再通过一个循环遍历houses列表中的每一处居民住宅。对于每一处居民住宅(坐标为(house_row, house_col)),计算当前位置((row, col))到该居民住宅的曼哈顿距离(在只能上下左右走的规则下,曼哈顿距离的计算公式为abs(row - house_row) + abs(col - house_col)),并累加到distance_sum变量中。
计算完当前位置到所有居民住宅的距离之和后,将distance_sum与min_distance_sum进行比较,如果distance_sum小于min_distance_sum,则更新min_distance_sum为distance_sum。
3. 输出
最后,将计算得到的最短距离之和min_distance_sum输出,它就是在平面方格图上设置一处便民办事处,使其到各个住宅位置的距离之和最短时的那个距离总和的值。
参考程序:
n = int(input("请输入居民住宅的数量: "))
# 用于存储居民住宅的坐标位置
houses = []
for _ in range(n):
x, y = map(int, input("请依次输入居民住宅的行坐标和列坐标,用空格隔开: ").split())
houses.append((x, y))
min_distance_sum = float('inf')
# 遍历整个方格图的每一个可能位置(这里简单假设方格图范围足够大,实际应用中可根据具体范围来限制)
for row in range(100): # 可以根据实际地图大小调整范围
for col in range(100):
distance_sum = 0
# 计算当前位置到所有居民住宅的距离之和
for house in houses:
house_row, house_col = house
# 计算曼哈顿距离(只能上下左右走时的距离计算方式)
distance_sum += abs(row - house_row) + abs(col - house_col)
min_distance_sum = min(min_distance_sum, distance_sum)
print(min_distance_sum)
本站内容未经许可,禁止任何网站及个人进行转载。









